Luna albastră sau Trei metode de determinare a dimensiunii

Noile tehnologii joacă un rol foarte important în activităţile educative. Multe astfel de instrumente sunt introduse în fiecare zi. Profesorul are rolul de a găsi care este cel mai potrivit instrument pentru atingerea obiectivelor urmărite în cadrul orelor de curs.

Determinarea dimensiunilor este unul dintre obiectivele unor lecţii de matematică. Această determinare se poate realiza clasic prin măsurare directă sau folosind noile tehnologii.

De exemplu, în clasa a VII-a, în cadrul orelor privind asemănarea triunghiurilor există problemele de determinare a înălţimilor prin măsurarea directă a umbrelor.

În cadrul unui proiectului eTwinning “The Magic Sky” , participând cu elevii la o activitate tip joc, privind înălţimea unor clădiri, am introdus o a doua metodă pe care am prezentat-o partenerilor noştri.

Astfel, am fotografiat şcoala şi un elev. Cunoscând înălţimea elevului, prin analiza fotografiei în programul Paint am putut determina înălţimea şcolii. Ne-am folosit de coordonatele furnizate de program pentru a stabili lungimea în pixeli a unor segmente şi, prin asemănarea triunghiurilor, ne-am atins obiectivul urmărit.

O altă activitate de acest gen a fost determinarea diametrului unor cratere lunare.

În acestă activitate am utilizat imaginea Lunii Albastre furnizată la data de 31.08.2012 de către cercetătorul Gianluca Masi, de la Observatorul Astronomic Bellatrix din Cecano, Italia.

Termenul  de Lună albastră este  folosit în mod obișnuit pentru a descrie o a doua lună plină într-o singură lună calendaristică, care se întâmplă o dată la doi-trei ani. Deci este un fenomen mai rar.

Folosind acestă imagine se pot determina dimensiunile diametrelor unor cratere lunare.

Prima metodă este cea în care elevii folosesc o linie gradată şi măsoară diametrul Lunii şi diametrul craterului vizat. Apoi , ştiind că diametrul real al Lunii este 3480 km, se poate determina diametrul real al craterului studiat.

A doua metodă este cea în care elevii folosesc programul Paint şi folosind coordonatele capetelor diametrelor ei pot afla lungimea diametrului Lunii şi a craterului în cauză. De exemplu , pentru craterul Tycho avem 600 pixeli/3480 km = 15 pixeli/x
Se obţine x = 87 km.

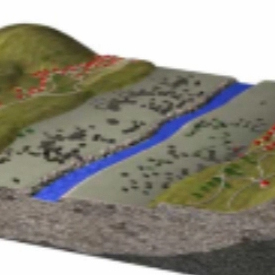
A treia metodă este metoda în care elevii utilizează programul SalsaJ.

Astfel, se deschide imaginea Lunii executând click pe <<Open>> din meniul <<File>>.

Se alege instrumentul <<Line>> din bara de instrumente şi se desenează diametrul Lunii. Programul SalsaJ va înregistra automat lungimea diametrului Lunii în pixeli.

Se selectează <<Set Scale>> din meniul <<Analyse>> şi se introduce lungimea reală a diametrului Lunii. În acest fel programul face raportul automat dintre lungimea în pixeli şi lungimea reală. Acum programul este pregătit pentru determinarea instantanee a dimensiunii oricărui crater dorim.

De exemplu, dacă dorim lungimea diametrului craterului Tycho , se selectează instrumentul <<Line>> din bara de instrumente şi se desenează diametrul craterului Tycho. Programul va afişa imediat, în bara de jos, lungimea diametrului desenat.

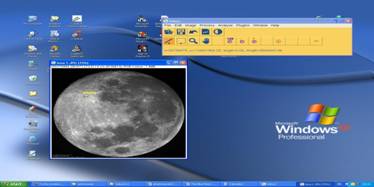
Programul SalsaJ este un software free al proiectului EU-HOU şi se găseşte la adresa web http://www.euhou.net/.

Prof. Kui Anisoara
Şcoala Gimnazială Vînători, Struct. Crivești
Jud. Iaşi